# Atcoder ABC143

# D - Bridges

我们有两个序列 $A_1,\ldots, A_M$ 和 $B_1,\ldots,B_M$ ，分别由 $1$ 和 $N$ （含）之间的内格组成。

对于由 "0" 和 "1" 组成的长度为 $M$ 的字符串，请考虑以下与该字符串对应的有 $2N$ 个顶点和 $(M+N)$ 条边的无向图。

这里， $i$ 和 $j$ 是整数，即 $1 \leq i \leq M$ 和 $1 \leq j \leq N$ ，顶点的编号为 $1$ 至 $2N$ 。

请找出一个长度为 $M$ 的字符串，由 "0" 和 "1" 组成，使得相应的无向图中的桥的数量最少。

关于桥的说明：桥是图中的一条边，删除它可以增加相连部分的数量。

关于桥的说明

桥是图中的一条边，删除它可以增加相连部分的数量。

数字 0 和 1 其实就是决定了连接 $a[i]与b[i]$ 的边是谁指向谁，也就是无向边定向。那么问题就转化成了决定无向边的方向，使得图中的桥最小。

其实这里有个地方需要注意，转化成连接 $a[i]与b[i]$ 是根据题目中的中间节点 $j+N$ 转化来的。根据例一，如果我们输出 00 ，那么这个图是这样的。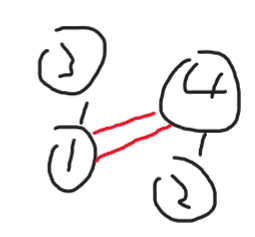

显而易见，他是有两个桥的。

如果是 01 则就一个桥都没有。

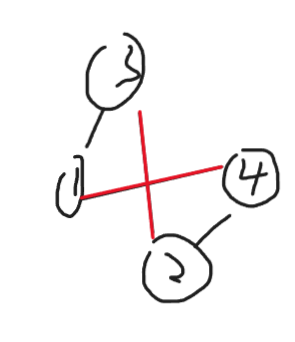
还有一个显而易见的，如果在无向图的情况下就出现了 “割边” 的情况，那么当它成为一个有向图那么它肯定还是割边，所以不用在意他的方向。

那么接下来思考如何给无向边定向，边双连通分量变成强联通分量，就是相当于在一棵树上多了几条返祖边，那么我们可以用 $DFS$ 序来建树，正常边向下，返祖边向上，再注意一下建的是双向边，所以两条边其实是一条边，记得判定一下就好。

建立双向边，跑 $DFS$ , 不走重复的边，不走走过的点，把答案记在边上，一条边为 0 ，另一条为 1 ，这样就结束啦。

Code

	#include <iostream>
	#include <algorithm>
	#include <cstring>
	#include <cstdio>
	#include <cmath>
	#include <map>
	#include <queue>
	#include <stack>
	#include <set>
	#include <iomanip>
	using namespace std;
	const int MAXN=1e6+10;
	struct edge{
	int nex,to,val,top;
	}p[MAXN];
	int head[MAXN],cnt=1,tot,num,dfn[MAXN],low[MAXN];//cnt 从一开始，那么第一条边的序号为 2，方便异或

	// 一开始还以为需要 tarjan，写了半天发现貌似用不到……
	bool vis[MAXN],vis1[MAXN];
	int a[MAXN],b[MAXN],belong[MAXN],ans[MAXN];
	stack<int>st;
	vector<int>dis[MAXN];
	void add(int from,int to,int val,int top){
	p[++cnt]=edge{head[from],to,val,top};
	head[from]=cnt;
	}
	void dfs2(int now,int fa){
	if(vis1[now]){
	return;
	}
	vis1[now]=true;
	for(int i=head[now];i;i=p[i].nex){
	int to=p[i].to;
	if(vis[i]){// 建的双向边
	continue;
	}
	vis[i^1]=vis[i]=true;
	ans[i]=1;
	ans[i^1]=0;
	dfs2(to,now);
	}
	return ;
	}
	int main(){
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=m;i++){
	cin>>a[i];
	}
	for(int i=1;i<=m;i++){
	cin>>b[i];
	}
	for(int i=1;i<=m;i++){
	add(a[i],b[i],i,a[i]);
	add(b[i],a[i],i,a[i]);
	}
	for(int i=1;i<=n;i++){
	if(!vis1[i]){
	dfs2(i,0);
	}
	}
	for(int i=1;i<=m;i++){
	cout<<ans[(i<<1)];
	}
	}