# 树形问题

为什么出这么一个博文呢：我今天听课以及题解看的不是很懂， $so$ 我想写个（~~现在还在上课但我没读题，下课补吧……~~）。

P2016 战略游戏
一道简简单单的树上 DP

不想点链接那么就看这里：

题意：他要建立一个古城堡，城堡中的路形成一棵无根树。他要在这棵树的结点上放置最少数目的士兵，使得这些士兵能瞭望到所有的路。
注意，某个士兵在一个结点上时，与该结点相连的所有边将都可以被瞭望到。
请你编一程序，给定一树，帮 $Bob$ 计算出他需要放置最少的士兵。

输入：第一行一个整数 $n$ ，表示树中结点的数目。

第二行至第 $n+1$ 行，每行描述每个结点信息，依次为：一个整数 $i$ ，代表该结点标号，一个自然数 $k$ ，代表后面有 $k$ 条无向边与结点 $i$ 相连。接下来 $k$ 个整数，分别是每条边的另一个结点标号 $r_1$ , $r_2$ , $\cdots,r_k$ $r1$ , $r2$ , $⋯$ , $rk$ , 表示 $i$ 与这些点间各有一条无向边相连。
对于一个 $n$ 个结点的树，结点标号在 0 到 $n−1$ 之间，在输入数据中每条边只出现一次。保证输入是一棵树。

输出：输出文件仅包含一个整数，为所求的最少的士兵数目。

正解肯定是得用 DP 嘛（毕竟开头就说了），所以我们根据题意设一个 $dp[u][0/1]$ 表示以 $u$ 为结点不放 / 放士兵，存的值为到该点不放 / 放时需要的士兵数量。

由题意可得，如果当前节点不放置士兵，那么它的子节点必须全部放置士兵，因为要满足士兵可以看到所有的边，所以
可以得出 $dp[u][0]=dp[u][0]+dp[to][1]$ ， $to$ 为 $u$ 的子节点。那为什么会这样呢？因为该点不放那么他的子节点就一定需要选，大家思考一下哦。

那么在该店放置士兵，那么不需要考虑它的子节点选不选，只要该点选了一定能看到子节点与该节点的所有路径（我们又是从下往上进行 dp，所以不需要管该点上面的那些节点），所以我们可以得到 $dp[u][1]+=min(dp[to][1],dp[to][0])+1$ 。

以上就是我们对这道题目的分析，以及状态转移方程的推出过程，以下只需要注意还需要建一个双向边。

Code：

	#include<iostream>
	using namespace std;
	struct edge{
	int nex,to;
	edge(int nex_=0,int to_=0){
	nex=nex_,to=to_;
	}
	}p[100100];
	int cnt=0,n,head[100100],dp[1010][1010];
	void add(int from,int to){// 个人感觉这么写链式前向星比较方便 (●'◡'●)
	p[++cnt]=edge(head[from],to);
	head[from]=cnt;
	}
	void dfs(int u,int fa){
	dp[u][1]=1,dp[u][0]=0;
	for(int i=head[u];i;i=p[i].nex){// 正常的遍历
	if(p[i].to==fa){
	continue;
	}
	dfs(p[i].to,u);// 正常的递归
	dp[u][0]+=dp[p[i].to][1];// 状态转移方程
	dp[u][1]+=min(dp[p[i].to][1],dp[p[i].to][0]);
	}
	}
	int main(){
	cin>>n;
	int x,y,z;
	for(int i=1;i<=n;i++){
	cin>>x>>y;// 与 x 这个点有 y 条连边
	for(int j=1;j<=y;j++){
	cin>>z;// 另一头为 z
	add(x,z);// 建一个双向边
	add(z,x);
	}
	}
	dfs(0,-1);
	cout<<min(dp[0][1],dp[0][0]);// 该点放或不放都会影响答案，所以取 min
	}

SP1437 PT07Z - Longest path in a tree

题意：求一棵无根树的直径。

如何求一棵树的直径呢：两边 dfs，第一次可以让一号节点为根节点，找到离他最远即深度最深的点，那么该点就为树的直径上的一个端点（不明白的可以自己推一下，画个树），那么再以该点为根节点进行 dfs 找到另一个点，则这个两个点中间的路径长就为树的直径（也就是另一个点的深度）。

板子题，直接附上代码。

Code：

	#include<iostream>
	using namespace std;
	struct edge{
	int nex,to;
	edge(int nex_=0,int to_=0){
	nex=nex_,to=to_;
	}
	}p[100010];
	int n,cnt=0,d[100100],maxx,head[100010];
	void add(int from,int to){// 存边（链式前向星）
	p[++cnt]=edge(head[from],to);
	head[from]=cnt;
	}
	void dfs(int now,int fa){
	d[now]=d[fa]+1;
	if(d[now]>d[maxx]){//（计算深度，如果深度比之前的最大深度还大，那么进行赋值
	maxx=now;
	}
	for(int i=head[now];i;i=p[i].nex){// 正常的遍历
	int to=p[i].to;
	if(to==fa){// 如果该点的下一个节点为自己的父亲，那么就跳过
	continue;
	}else{
	dfs(to,now);// 不断遍历
	}
	}
	}
	int main(){
	cin>>n;
	int x,y;
	d[0]=-1;
	for(int i=1;i<n;i++){
	cin>>x>>y;
	add(x,y);
	add(y,x);// 双向存边
	}
	dfs(1,0);// 第一次是从 1 号节点出发
	dfs(maxx,0);// 第二次是从记录的最深的地方为根节点
	cout<<d[maxx]<<endl;
	return 0;
	}

P3252 [JLOI2012] 树

题目描述：在这个问题中，给定一个值 $s$ 和一棵树。在树的每个节点有一个权值，第 $i$ 个点的权值为 $a_i$ ，问有多少条路径的节点权值总和为 $s$ 。路径中节点的深度必须是升序的。假设节点 1 是根节点，根的深度是 0 ，它的儿子节点的深度为 1 。路径不必一定从根节点开始。

既然要求深度是升序的，我们可以枚举每一个点开始遍历，设一个 $val$ 记录当前的权值和，如果它比 $s$ 大了，直接结束递归。

Code：

	#include<iostream>
	using namespace std;
	int n,s,cnt,ans;
	struct edge{
	int nex,to;
	edge(int nex_=0,int to_=0){
	nex=nex_,to=to_;
	}
	}p[200100];
	int head[100100],fa[100100],v[100100];
	void add(int from,int to){// 存边（链式前向星）
	p[++cnt]=edge(head[from],to);
	head[from]=cnt;
	}
	void dfs(int now,int val){// 注意这里不是传的 fa 而是传的目前的权值和
	if(val>s){// 如果大了直接结束
	return;
	}
	if(val==s){
	ans++;
	return ;
	}
	for(int i=head[now];i;i=p[i].nex){
	int to=p[i].to;
	if(to==fa[now]){// 下一个点为自己的父亲，那么就跳过
	continue;
	}
	dfs(to,val+v[to]);
	}
	}
	int main(){
	cin>>n>>s;
	for(int i=1;i<=n;i++){
	cin>>v[i];
	}
	int x,y;
	for(int i=1;i<n;i++){
	cin>>x>>y;
	add(x,y);
	fa[y]=x;// 记录父亲
	}
	for(int i=1;i<=n;i++){
	dfs(i,v[i]);// 每一个为头点进行遍历
	}
	cout<<ans<<endl;
	}

P6591 [YsOI2020] 植树

题意：有一棵 $n$ 个节点的无根树 $T$ ，它是一个没有环的无向联通图，发现一个节点如果可以成为根，它必须十分平衡，这意味着以它为根时，与它直接相连的节点，他们的子树大小都相同，让你求出所有能作为根的节点编号。

题解中讲解更详细哦～

P6591 题解

用一个样例来说一说吧（题解里的）。

输入：

输出：

5 6 7

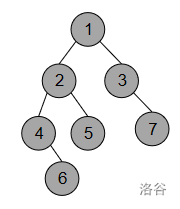
以 1 为根，计算各结点的子树大小（包含自己）：

7 4 2 2 1 1 1

然后让每个节点找自己子结点的子树大小，以及 $n$ 减去自己大小的值：

我们看到，只有第 5 , 6 , 7 行的数字完全相同，满足条件，所以输出 5 6 7

Code:

	#include<iostream>
	using namespace std;
	int n;
	struct edge{
	int nex,to;
	edge(int nex_=0,int to_=0){
	nex=nex_,to=to_;
	}
	}p[2001000];
	int root[2000100],cnt,head[2000100],d[2000100];//d [x] 表示 x 的子树大小，root [x] 表示是否可以作为根。
	void add(int from,int to){
	p[++cnt]=edge(head[from],to);
	head[from]=cnt;
	}
	int dfs(int now,int fa){
	root[now]=1;
	int num=0;// 记录所连各节点的子树大小，配合下文注释与代码理解
	for(int i=head[now];i;i=p[i].nex){
	int to=p[i].to;
	if(to==fa){
	continue;
	}
	d[now]+=dfs(to,now);
	if(!num){// 记录第一个所连节点的子树大小
	num=d[to];
	}
	if(num!=d[to]){// 如果与先前的不一样，说明不满足条件，直接 root=0
	root[now]=0;
	}
	}
	d[now]++;
	if(now!=1&&num&&num!=n-d[now]){// 判断 n−d [x] 是否和 num 相等，这一条不好想。
	root[now]=0;
	}
	return d[now];
	}
	int main(){
	cin>>n;
	int x,y;
	for(int i=1;i<n;i++){
	cin>>x>>y;
	add(x,y);// 双向边
	add(y,x);
	}
	dfs(1,0);
	for(int i=1;i<=n;i++){
	if(root[i]){// 为 true (也就是 1) 就输出
	cout<<i<<" ";
	}
	}
	}

# 未完待续（To Be Continue）……

树

# 树形问题

# 未完待续（To Be Continue）……

轻重链剖分